Floating-Point Formats
Here are several different formats adopted by different machines.
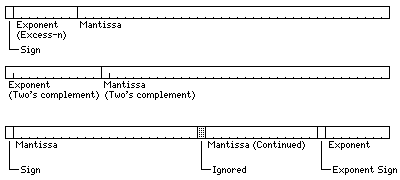
The format shown in the first line begins with a single sign bit, which is 0
if the number is positive, and 1 if the number is
negative. Next is the exponent. If the exponent is eight bits long, as shown in
the diagram, it is in excess-128 notation, so that the smallest exponent value,
00000000, stands for -128, and the largest exponent value, 11111111, stands for
127. Finally, we find the mantissa, which is an unsigned binary fraction.
If the mantissa is normalized, non-negative floating-point numbers can be
compared by the same instructions as are used to compare integers.
This format is particularly popular on computers that have hardware support
for floating-point numbers. A number of variations on this format are used.
Of course, the length of the exponent field shown in the diagram is only one
possibility.
The second line in the diagram illustrates the kind of floating-point format
used on computers such as the PDP-8 and the RECOMP II. Here, a floating-point
number is simply represented by two signed binary numbers, the first, being the
exponent, treated as an integer, and the second, being the mantissa, treated as
a fraction, both represented in the ordinary format for signed fixed-point
numbers used on the computer.
The third line of the diagram illustrates a kind of format which, with a
number of variations, was found on most computers with a 24-bit word length.
Computers with a 48-bit word length, on the other hand, typically had hardware
floating-point, and used a floating-point format of the type given in the first
line.
Why did these computers use such an unusual floating-point format?
Typically, although these computers did not have hardware floating-point
support, the way bigger computers with a 32-bit, 36-bit, 48-bit, or 64-bit word
length did, they did come standard with hardware integer multiplication, unlike
smaller computers with an 18-bit, 16-bit, or 12-bit word length.
In order to support floating-point arithmetic, the format of
double-precision fixed-point numbers on most of these computers omitted the
first bit of the second word of the number from the number itself, sometimes
treating it as a second copy of the sign, so that fixed-point numbers could be
treated as having the binary point on the right, making them integers, or on
the left, after the sign, making them fractions on the interval [0,1), without
having to adjust them by shifting them one place to the left after a
multiplication.
A number of variations of each type of floating-point format exist, of
course. When a floating-point format consists of a mantissa field followed by
an exponent field, with no omitted bit, the choice of whether to consider the
floating-point format as belonging to Group II or Group
Group I Floating-Point Formats
The diagram below shows several examples of floating-point formats of the
first type, but they are only a very small sampling of the number of formats of
this type that have been used.

The
The PDP-10 (and its compatible relatives, the PDP-6 and the DECSYSTEM-20)
and the Xerox Sigma computers (which, like the System/360, also used a
hexadecimal exponent), which both used two's complement notation for integers,
performed a two's complement on the combined exponent and mantissa fields of a
floating-point number when it was negative. This meant that all normalized
floating-point numbers, whether they were positive or negative, could be
compared by integer compare instructions, producing correct results.
The Control Data 1604 computer used an exponent field that was 11 bits long;
also, it used one's complement notation for integers, and the mantissa (called
the coefficient in that computer's manuals) of floating-point numbers
was also complemented for negative numbers. This same representation of
negative numbers was used on the Control Data 6600, but for a 60-bit
floating-point number, again with an 11-bit exponent.
The diagram depicts the exponent as being in excess-1024 notation; actually,
that is not quite accurate. Because of its use of one's complement notation for
integers, to use the same type of circuitry for arithmetic on exponents, zero
and positive exponents were represented in excess-1024 notation, but negative
exponents were represented in excess-1023 notation. Thus, on the Control Data
1604, the exponent value of octal 1777 was not used. On the Control Data 6600,
the exponent value of 3777 octal represented an overflow, the exponent value of
0000 octal represented an underflow, and the exponent value of 1777 octal
represented an indeterminate quantity. The exponent here is shown as in
excess-976 notation, with the binary point located at the beginning of the
mantissa field as with the other formats shown here, since it was considered to
be in excess-1024 (or excess-1023) notation, but with the binary point at the
end of the mantissa, which was considered to be an integer.
The AN/FSQ-32 computer, built by
The Cray-1, on the other hand, had a sign bit, 15 bits of excess-16,384
exponent, and 48 bits of mantissa using the more common sign-magnitude format
for floating-point numbers.
Other computers, such as the PDP-11, and its successor, the VAX, dealt with
the wastefulness of having the first bit of the mantissa (almost) always one by
omitting that bit from the representation of a number. The number zero was
still represented by a zero mantissa combined with the lowest possible exponent
value; thus, this exponent value had to be given the additional meaning that
the hidden one bit was not present. The diagram above shows only one of the
formats used with the PDP-11, although in single precision it was called the F
format, and in double precision, the D format, on the VAX and on the Alpha;
other formats were used, including the G format, which had an exponent field
that was 11 bits in length, used in a 64-bit floating-point number, and which
led to the expanded range format for the PDP-10 which is shown above, and the H
format, which had an exponent field 15 bits in length, and which was used in a
128-bit floating-point number. Of course, the Alpha now also supports the
standard IEEE-754 floating-point format, which is described here as the
"Standard" floating-point format. As well, the earliest software
floating-point provided for the first PDP-11 belonged instead to Group II, and
involved a 16-bit two's complement exponent followed by a 32-bit two's
complement mantissa.
The current standard floating-point representation used in today's
microcomputers, as specified by the IEEE 754 standard, is based on that of the
PDP-11, but in addition also allows gradual underflow as well. This is achieved
by making the lowest possible exponent value special in two ways: it indicates
no hidden one bit is present, and in addition the value represented by the
floating-point number is formed by multiplying the mantissa by the power of two
that the next lower exponent value also indicates. It is therefore considerably
more complicated than the way in which floating-point numbers were typically
represented on older computers.
In the
The Burroughs 5500, 6700, and related computers used an exponent which was a
power of eight. The internal format of a single-precision floating-point number
consisted of one unused bit, followed by the sign of the number, then the sign
of the exponent, then a six-bit exponent, then 39-bit mantissa. The bias of the
exponent was such that it could be considered to be in excess-32 notation as
long as the mantissa was considered to be a binary integer instead of a binary
fraction. This allowed integers to also be interpreted as unnormalized
floating-point numbers.
A double-precision floating-point number had a somewhat complicated format.
The first word had the same format as a single-precision floating-point number;
the second word consisted of nine additional exponent bits, followed by 39
additional mantissa bits; in both cases, these were appended to the bits in the
first word as being the most significant bits of the number.
It may also be noted that the MANIAC II computer used a floating-point
format where the exponent was a power of 65,536. This reduced the number of
shifts required, which was very important on a very early vacuum-tube computer,
although the maximum possible loss of precision was rather drastic on a machine
with a 48-bit word length. But the machine performed floating-point arithmetic
only, and it used only a four-bit field for the exponent and its sign; thus,
the intent behind its floating-point format can be considered to be one of
using a format that is halfway between conventional floating-point format and
integer format, so as to obtain the extended range of the former with the speed
of the latter.
The BRLESC computer, with a 68-bit word length, used a base-16 exponent; it remainined within the bounds of convention, as the word
included a three-bit tag field, followed by a one-bit sign; then, for a
floating-point number, 56 bits of mantissa followed by 8 bits of exponent.
Thus, the 68-bit word contained 65 data bits and three tag bits, while the
whole 68-bit word was used for an instruction. (In addition, four parity bits
accompanying each word were usually mentioned.)
The historic English Electric KDF9 computer used a floating-point format very
similar to that of the
The Foxboro
The Packard-Bell 440 computer was microprogrammable,
but its design was optimized for the floating-point format shown here, which
belongs to Group I, although, as is the case for some other Group I formats, it
includes an omitted sign bit in the second word.
Group II Floating-Point Formats
Some of the formats of the type given in the second line of the diagram at
the top of the page are illustrated below:
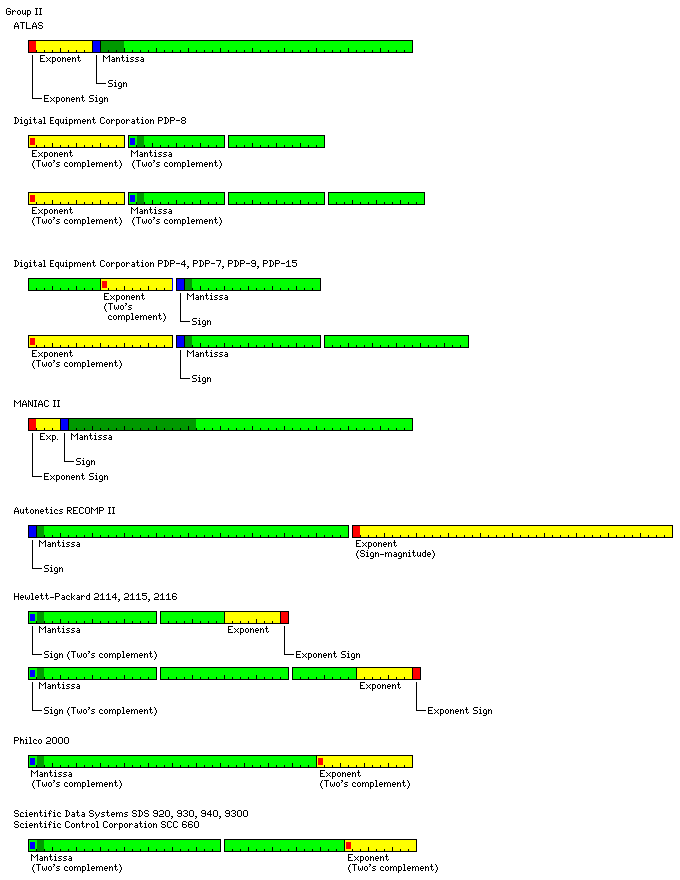
The floating-point hardware optionally available for the PDP-8, called the
Floating Point Processor-12, as it was originally introduced as an option for
the PDP-12 (an updated version of the LINC-8), and a set of floating-point
routines for the PDP-8 available as a separate product, both used a single
12-bit word for the exponent, and multiple 12-bit words to represent the
mantissa. Other floating-point representations also were used in software on
the PDP-8, however; for example, 8K FORTRAN used a format which began with one
bit for the sign of the number, followed by an eight-bit signed exponent, with
the first three bits of the mantissa completing the first word; this format
belonged to the class illustrated by the first line of the diagram above, and
was used in order to provide compatibility with the PDP-10 and/or the
Double-precision floating-point numbers on the PDP-4, 7, 9 and 15 were represented
by one 18-bit word for the exponent, and two 18-bit words containing the
mantissa; the format of single-precision floating-point numbers on those
machines was more complicated, and therefore of a form which does not fully
belong to any of the three groups examined here, but which allowed quick
conversion to the double-precision floating-point format by first appending a
copy of the first word as the third word, and then performing masking and, in
the case of the exponent, sign extension.
The
The Scientific Control Corporation 660 computer used two's complement
notation for integers, and also produced a 48-bit fraction when it multiplied
two 24-bit fixed-point numbers, and its floating-point format also consisted of
a 39-bit two's complement mantissa followed by a 9-bit two's complement
exponent.
The RECOMP II, a drum-based computer with a 40-bit word length, simply used
one 40-bit word for the exponent, and one 40-bit word for the mantissa.
(Incidentally, it used sign-magnitude notation for numbers, not two's
complement.) While this was obviously done merely to simplify the design of the
computer, advertisements (appearing, for example, in Scientific American
during the late 1950s) extolled the ability of this computer to handle numbers
which, if written down, would girdle the entire globe.
This diagram does not show all the formats of this type that were in use;
the Paper Tape Software Package for the PDP-11 included a Math Package with
floating-point routines that worked on a format consisting of a 16-bit two's
complement exponent followed by a 32-bit two's complement mantissa.
Also, the Manchester ATLAS computer, notable for introducing virtual memory,
used an 8-bit sign-magnitude exponent followed by a 40-bit sign-magnitude
mantissa. The exponent was a power of eight. A power-of-eight exponent was also
used on the Burroughs 5500; thus, a claim I once read that a power-of-eight
exponent did not, in practice, lead to the type of
problems encountered with the power-of-sixteen exponent on the
Another floating-point format that belongs to this class was used with the
Hewlett-Packard 2114/5/6 computers. A floating-point number began with a two's
complement mantissa, and then ended with seven bits of exponent, followed
by the sign of the exponent, neither of which was complemented when the number
was negative. Floating-point numbers could occupy either two or three 16-bit
words, depending on whether they were single or double precision.
Group III Floating-Point
Formats
The floating-point formats of many 24-bit computers followed the model shown
in the third line of the diagram at the top of the page, but they varied in
minor ways from it, and are illustrated below.
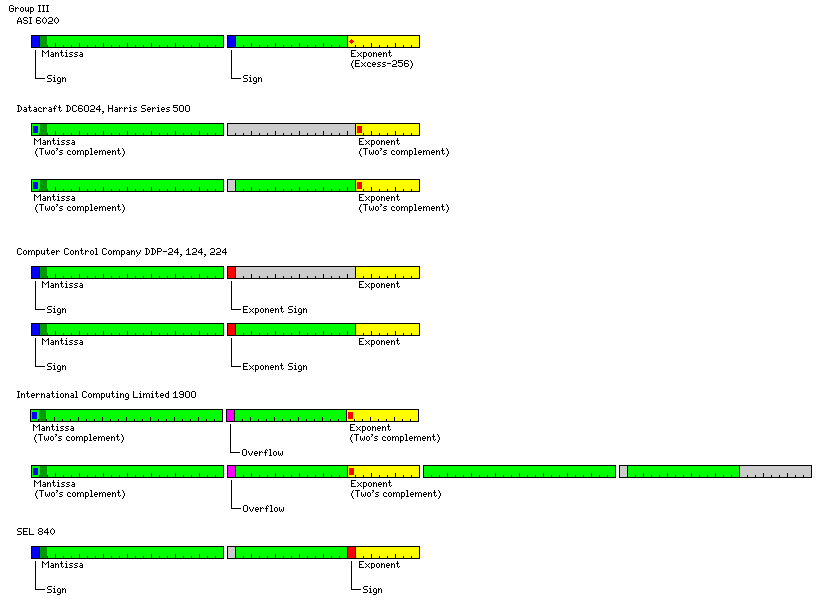
The
The Datacraft 6024 computer, and its successors
from Harris, used two's complement form to represent integers. The exponent
field, including sign, was eight bits long. The basic format shown above was
used for double-precision floating-point; in single-precision floating point,
numbers still occupied two 24-bit words in memory, but the portion of the
mantissa in the second word was not used.
The DDP-24 computer, from 3C and then Honeywell, used sign-magnitude
representation for integers, and a multiply instruction ensured both words of
the product contained the same sign. It also left the mantissa portion of the
second word unused for single-precision numbers. The eight least significant
bits of the second word contained the value of the exponent; the sign of the
exponent was contained in the sign bit of the second word, instead of that bit
being unused.
The
The SEL 820 computer, which I believe to be the last of the major members of
the "classic" group of 24-bit computers to be described on these
pages (here, I am thinking primarily of the Datacraft
DC 6024, the Computer Controls Corporation DDP 224, the
A Final Comment
Note also that the three lines in the first diagram which illustrated the
three possible general types of format, as well as the illustrations of
floating-point formats in the other diagrams, assume that the component parts
of the floating-point number, whether they are 24-bit words or 8-bit bytes, are
lined up so as to be in the normal left to right direction from most
significant to least significant for representing integers. Thus, on a little-endian
machine, the component of the number on the left would be at a location with a
higher address instead of a lower one. Note, however, that on at least some
machines, while integers were represented in little-endian form, floating-point
numbers were represented in big-endian form.
On the PDP-11, a particularly unfortunate variation of this took place. As
it was the first computer to attempt to achieve the consistent use of a
little-endian representation for data (previous computers were always
big-endian when packing characters into words, but sometimes were little-endian
when using two words to represent a long integer) this novel concept was
doubtless unfamiliar to the engineers designing the FP-11, the initial hardware
floating-point unit designed for this architecture.
The PDP-11 had a 16-bit word, but could also address and manipulate 8-bit
bytes directly. As with many other computers, such as the Honeywell 316, a
32-bit integer was stored with its least significant 16-bit word first, in the
lower memory address, so that addition could begin while the more significant
words of the operands were being fetched. However, unlike other computers in
existence at the time, for consistency, the PDP-11 was designed so that the
least significant 8 bits of a 16-bit word had the lower byte address, and the
more significant 8 bits of a 16-bit word had the higher byte address.
Because the FP-11 was designed as though the PDP-11 were a big-endian
computer instead of a little-endian computer, it placed the most significant 16
bits of the values on which it acted in the 16-bit word at the lowest memory
address, the next less significant 16 bits in the 16-bit word at the next
higher memory address, and so on.
In addition to floating-point numbers, this included 32-bit integers as
well, but as the PDP-11 already posessed instructions
to assist in handling 32-bit integers in little-endian format, this flaw was
corrected in subsequent extensions to the PDP-11 architecture. The
floating-point format, however, remained unaltered.
The byte addressing within a word was a property of the base PDP-11
architecture, and was not altered by the design of the FP-11 as though it were
for a big-endian machine. The most significant bit within a 16-bit word inside
the FP-11 was still transmitted to the most significant bit of a 16-bit word
inside the PDP-11. Hence, in the illustrations of the floating-point format for
the PDP-11 shown above, the successive bytes in a floating-point number have
addresses in the order:
1 0 3 2 5 4 7 6
instead of
7 6 5 4 3 2 1 0
as is the case on a consistently little-endian
machine, as it had been intended to make the PDP-11, or
0 1 2 3 4 5 6 7
as they would be on a consistently big-endian
machine, like the
This aspect of the PDP-11 floating-point format was preserved, at least for the F and D formats, even on the VAX computer, because it included a PDP-11 compatibility mode.